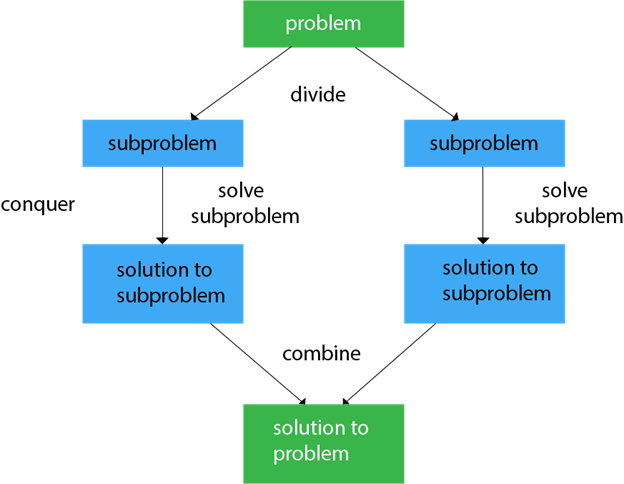
Divide and conquer là một trong số những mẫu thiết kế giải thuật chung được nhiều người biết đến nhất, và merge sort là một ứng dụng hay được tạo ra trên nền algorithm này. Trước khi đến với thuật toán Merge Sort, chúng ta hãy tìm hiểu về Divide and Conquer.
Divide and conquer technique (typical case)
Các giải thuật devide and conquer hoạt động theo các bước sau:
1. Problem sẽ được chia thành nhiều cụm nhỏ, nên có kích thước bằng nhau.
2. Chúng ta sẽ xử lý tuần tử các problem nhỏ, đa số dùng đệ quy.
3. Trong một số trường hợp, kết quả của chúng sẽ được gộp để có kết quả.
Một ví dụ đơn giản khi chúng ta muốn tính tổng n số hạng từ a0,… a(n-1) với điều kiện n>1. Chúng ta sẽ chia nhỏ bài toán thành hai bài toán nhỏ hơn: tính tổng từ đầu đến n/2 và từ n/2 hết phần còn lại. Và tiếp tục sử dụng đệ quy cho đến khi không thể chia nhỏ được nữa.
Giải thuật toán Merge Sort
Merge sort là một ví dụ của giải thuật divide and conquer này. Sau khi chia đủ nhỏ, merge sort sẽ gộp hai dữ liệu đã sort thành một dữ liệu lớn hơn.
Streamhub
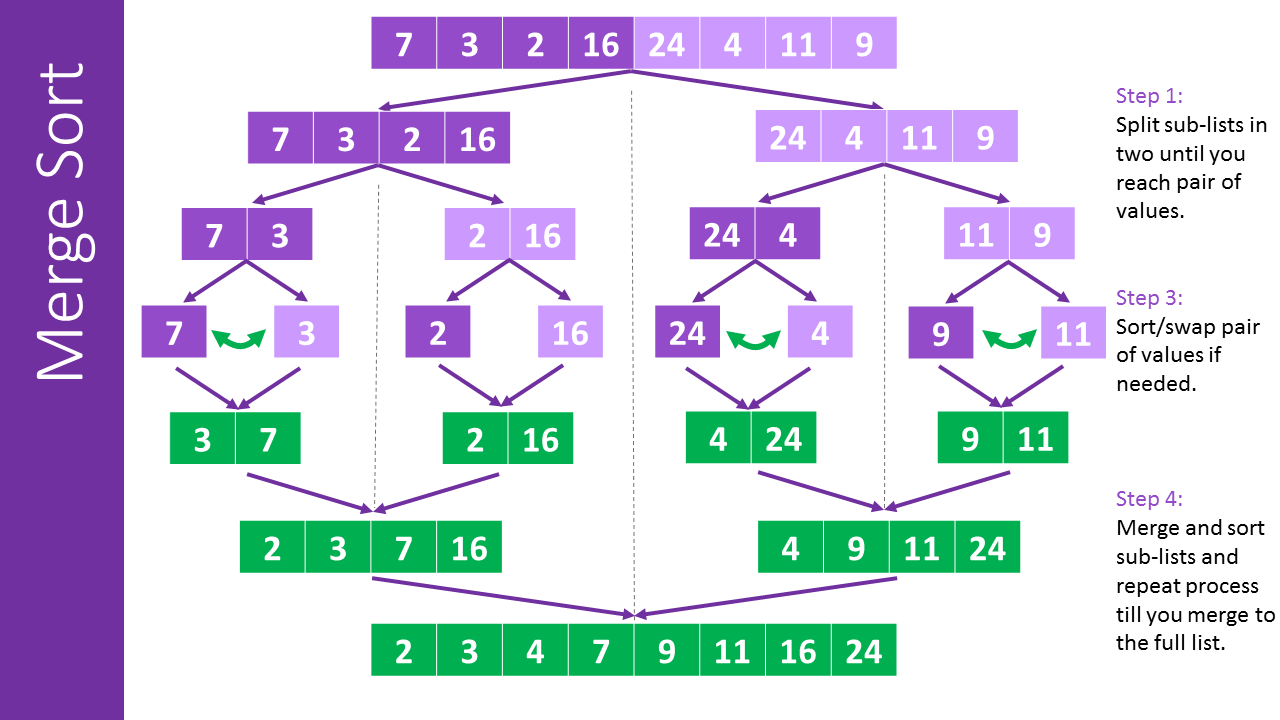
Theo hình trên, bạn có thể dễ dàng nhận ra cách chia nhỏ bài toán và gộp lại để cho ra kết quả.
Độ phức tạp của thuật toán merge sort
Với n là số mũ của 2 và C(n) là số lần so sánh n phần tử, ta có:
C(n) = 2C(n/2) + Cmerge(n) for n>1, C(1) = 0
Tại sao như vậy?
Ví dụ: chúng ta cần sử dụng merge sort đế sort 8 chữ số sau theo thứ tự tăng dần:
Bước 1: Chia ra (divide)
Lần chia 1: 1 dãy số
108 15 50 4 8 42 23 16
Lần chia 2: 2 dãy số
(108 15 50 4) (8 42 23 16)
Lần chia 3: 4 dãy số
(108 15) (50 4) (8 42) (23 16)
Lần chia 4: 8 dãy số
(108) (15) (50) (4) (8) (42) (23) (16)
Trong đó: C(n/2) là số so sánh chúng ta cần khi chia nửa số hạng, và cần 2 lần như vậy cho mỗi bước. Do đó ta có 2C(n/2)
Bước 2: Merge (conquer)
Lần gộp 1 – Số lần so sánh mỗi cặp tối đa: 1
(108) (15) (50) (4) (8) (42) (23) (16)
Lần gộp 2 – Số lần so sánh mỗi cặp tối đa: 1
(15 108) (4 50) (8 42) (16 23)
Lần gộp 3 – Số lần so sánh mỗi cặp tối đa: 4
(4 15 50 108) (8 16 23 32)
Ở bước này, xét trong hai cặp (15 108) và (4 50), merge sort sẽ lấy từng phần tử bé nhất của mỗi list (hoặc array) so sánh với nhau.
Cho A {15, 108} và B {4, 50}, các bước so sánh theo tuần tự:
15 và 4: 4 nhỏ hơn → {4} ; A {15, 108} ; B {50}
15 và 50: 15 nhỏ hơn → {4, 15} ; A {108} ; B {50}
108 và 50: 50 nhỏ hơn → {4, 15, 50} ; A {108} ; B {}
Chỉ còn 108 → {4, 15, 50, 108}
Tương tự với dãy array còn lại.
Lần gộp 4 – Số lần so sánh mỗi cặp tối đa: 8
(4 8 15 16 23 32 50 108)
Do vậy trong trường hợp xấu nhất, ta có n-1 lần so sánh.
Do đó ta có C(n) = 2C(n/2) + n -1 với n >1
Rút gọn lại: C(n) = 2C(n/2) + n
Giải theo Master Theorem, ta có kết quả O(nlogn)
Code của thuật toán Merge Sort
procedure mergesort(1,r: integer);
var i, j, k, m : integer;
begin
if r-1>0 then
begin
m:=(r+1)/2; mergesort(1,m); mergesort(m+1,r);
for i := m downto 1 do b[i] := a[j];
for j :=m+1 to r do b[r+m+1-j] := a[j];
for k :=1 to r do
if b[i] < b[j] then
begin a[k] := b[i] ; i := i+1 end
else begin a[k] := b[j]; j:= j-1 end;
end;
end;
Ưu điểm và nhước điểm của Merge Sort
Ưu: Độ phức tạp tốt hơn so với Insertion Sort, Selection Sort, Interchange Sort
Nhược: Cần thêm bộ nhớ để chứa một mảng thứ 3
Tham khảo thêm về Merge Sort tại video ngắn sau đây: